

1、单选题:
函数![]() 的所有间断点是( )。
的所有间断点是( )。
选项:
A:
![]() ,其中
,其中![]()
B:
![]() ,其中
,其中![]()
C:
![]() ,其中
,其中![]()
D:
![]() ,其中
,其中![]()
答案: 【
![]() ,其中
,其中![]()
】
2、单选题:
极限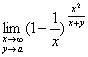 的值是( )。
的值是( )。
选项:
A:0
B: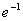
C:e
D:1
答案: 【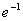 】
】
3、单选题:
极限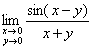 的值是( )。
的值是( )。
选项:
A:∞
B:1
C:0
D:不存在
答案: 【不存在】
4、单选题:
设函数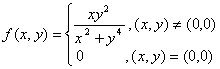 ,则( )。
,则( )。
选项:
A:极限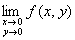 不存在
不存在
B:极限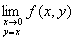 不存在
不存在
C:极限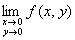 存在,但
存在,但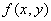 在点(0,0)处不连续
在点(0,0)处不连续
D: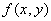 在点(0,0)处连续
在点(0,0)处连续
答案: 【极限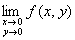 不存在】
不存在】
5、单选题:
函数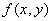 在点
在点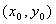 偏导数存在是
偏导数存在是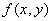 在该点连续的( )。
在该点连续的( )。
选项:
A:既不是充分条件,也不是必要条件
B:必要条件,但不是充分条件
C:充分条件,但不是必要条件
D:充分必要条件
答案: 【既不是充分条件,也不是必要条件】
6、单选题:
设函数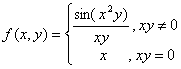 则
则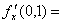 ( )。
( )。
选项:
A:2
B:0
C:不存在
D:1
答案: 【1】
7、单选题:
设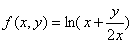 ,则
,则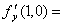 ( )。
( )。
选项:
A:0
B:1
C: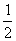
D:2
答案: 【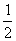 】
】
8、单选题:
设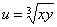 ,则
,则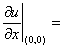 ( )。
( )。
选项:
A:1
B:不存在
C:-1
D:0
答案: 【0】
9、单选题:
设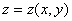 是由方程
是由方程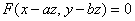 所确定的函数,其中
所确定的函数,其中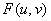 是变量u,v的任意可微函数,a,b为常数
是变量u,v的任意可微函数,a,b为常数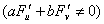 ,则必有( )。
,则必有( )。
选项:
A: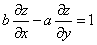
B: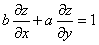
C: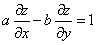
D: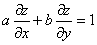
答案: 【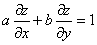 】
】
10、单选题:
已知函数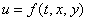 ,其中
,其中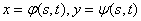 ,并且这些函数均有一阶连续偏导数,那么
,并且这些函数均有一阶连续偏导数,那么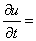 ( )。
( )。
选项:
A: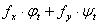
B: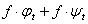
C: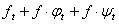
D: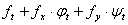
答案: 【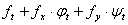 】
】
11、单选题:
设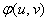 有连续的偏导数,
有连续的偏导数,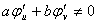 且
且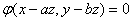 ,则
,则 =( )。
选项:
A:b
B:a
C:-1
D:1
答案: 【1】
12、单选题:
设函数u=xyz在点(1,1,2)的某邻域内可微分, 则函数u在点(1,1,1)处的梯度为( )。
选项:
A:
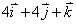
B:5
C: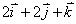
D:3
答案: 【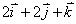 】
】
13、单选题:
曲线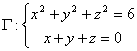 在点
在点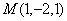 的切线一定平行于( )。
的切线一定平行于( )。
选项:
A: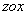 平面
平面
B: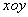 平面
平面
C: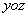 平面
平面
D:平面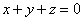
答案: 【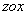 平面】
平面】
14、单选题:
曲面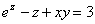 在点
在点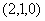 处的切平面方程为( )。
处的切平面方程为( )。
选项:
A: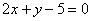
B: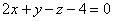
C: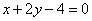
D: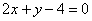
答案: 【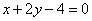 】
】
15、单选题:
空间曲线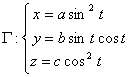 ,在点
,在点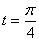 处的法平面必( )。
处的法平面必( )。
选项:
A:平行于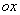 轴
轴
B:垂直于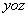 平面
平面
C:垂直于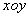 平面
平面
D:平行于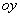 轴
轴
答案: 【平行于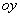 轴】
轴】
16、单选题:
曲线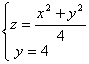 在点
在点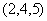 处的切线与横轴的正向所成的角度是( )。
处的切线与横轴的正向所成的角度是( )。
选项:
A: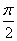
B: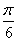
C: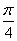
D: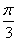
答案: 【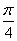 】
】
17、判断题:
函数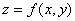 在点
在点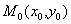 的全微分就是曲面
的全微分就是曲面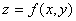 在点
在点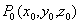 的切平面上的点
的切平面上的点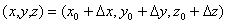 的
的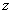 坐标的改变量
坐标的改变量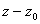 。( )
。( )
选项:
A:错
B:对
答案: 【对】
18、判断题:
设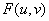 具有连续偏导数,则曲面
具有连续偏导数,则曲面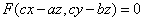 的切平面平行于一定直线,其中
的切平面平行于一定直线,其中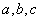 为常数。( )
为常数。( )
选项:
A:对
B:错
答案: 【对】
19、判断题:
函数在某点的方向导数存在, 则函数在此点的偏导数存在。( )
选项:
A:错
B:对
答案: 【错】
20、判断题:
函数沿其梯度方向的方向导数达到最大值, 且最大值为梯度的模。( )
选项:
A:错
B:对
答案: 【对】
21、判断题:
若函数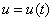 及
及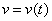 都在点
都在点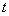 可导, 函数
可导, 函数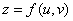 在对应点
在对应点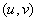 具有连续偏导数, 则复合函数
具有连续偏导数, 则复合函数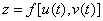 在点
在点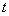 可导, 且其导数为
可导, 且其导数为 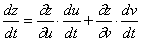 。( )
。( )
选项:
A:错
B:对
答案: 【对】
22、判断题:
设 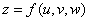 与
与 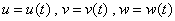 复合而得到函数
复合而得到函数 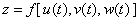 .若
.若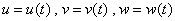 在点
在点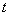 可导,
可导, 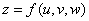 对
对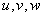 具有连续偏导数, 则复合函数
具有连续偏导数, 则复合函数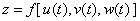 在点
在点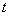 可导, 且
可导, 且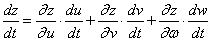 。( )
。( )
选项:
A:对
B:错
答案: 【对】
23、判断题:
若函数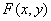 满足的偏导数
满足的偏导数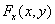 ,
, 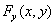 在点
在点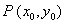 的某邻域内
的某邻域内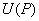 内连续;则在
内连续;则在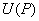 内, 方程
内, 方程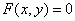 必能唯一确定一个定义在点
必能唯一确定一个定义在点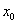 的某邻域
的某邻域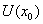 内的一元单值函数
内的一元单值函数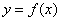 , 使得
, 使得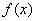 在
在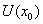 内有连续导函数
内有连续导函数 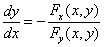 。( )
。( )
选项:
A:错
B:对
答案: 【错】
24、判断题:
偏导数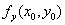 表示曲面
表示曲面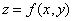 被平面
被平面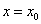 所截得的曲线
所截得的曲线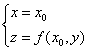 在点
在点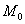
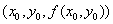 处的切线对
处的切线对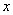 轴的斜率。( )
轴的斜率。( )
选项:
A:对
B:错
答案: 【错】
25、判断题:
函数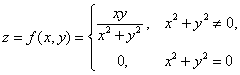 在点
在点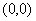 处是连续的且偏导数也是存在的。( )
处是连续的且偏导数也是存在的。( )
选项:
A:错
B:对
答案: 【错】
26、判断题:
二元函数在一点不连续, 但其偏导数一定存在。( )
选项:
A:对
B:错
答案: 【错】
27、判断题:
如果函数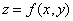 的两个二阶混合偏导数
的两个二阶混合偏导数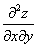 及
及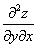 在区域内存在, 那么在该区域内这两个二阶混合偏导数必相等。( )
在区域内存在, 那么在该区域内这两个二阶混合偏导数必相等。( )
选项:
A:对
B:错
答案: 【错】
28、判断题:
若二元函数的两个累次极限与重极限都存在,则三者必相等。( )
选项:
A:对
B:错
答案: 【对】
29、判断题:
若二元函数的两个累次极限存在,但不相等,则二重极限可能存在。( )
选项:
A:错
B:对
答案: 【错】
30、判断题:
不存在由闭区间到圆周上的一对一连续对应。( )
选项:
A:错
B:对
答案: 【对】

备案号:冀ICP备20010840号 2020-2099辉辉网络科技 All Rights Reserved