

1、判断题:
方程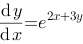 是一个可分离变量的微分方程.
是一个可分离变量的微分方程.
选项:
A: 正确
B: 错误
答案: 【 正确】
2、判断题:
方程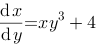 是一个一阶线性微分方程.
是一个一阶线性微分方程.
选项:
A: 正确
B: 错误
答案: 【 正确】
1、单选题:
微分方程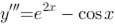 的通解为( ).
的通解为( ).
选项:
A: 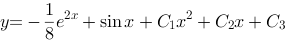
B: 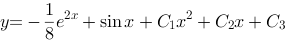
C: 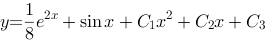
D: 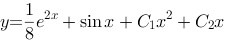
答案: 【 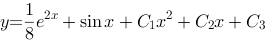 】
】
1、判断题:
方程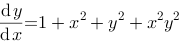 是一个可分离变量的微分方程.
是一个可分离变量的微分方程.
选项:
A: 正确
B: 错误
答案: 【 正确】
2、判断题:
方程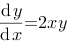 的通解为
的通解为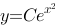 .
.
选项:
A: 正确
B: 错误
答案: 【 正确】
1、单选题:
微分方程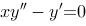 的通解为( ).
的通解为( ).
选项:
A: 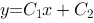
B: 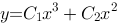
C: 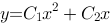
D: 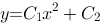
答案: 【 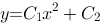 】
】
2、判断题:
微分方程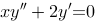 满足初始条件
满足初始条件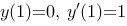 的特解为
的特解为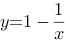 .
.
选项:
A: 正确
B: 错误
答案: 【 正确】
1、判断题:
表示未知函数、未知函数的导数与自变量之间的关系的方程称为微分方程.未知函数是一元函数的,称之为常微分方程.
选项:
A: 正确
B: 错误
答案: 【 正确】
2、判断题:
微分方程通解中任意常数都被初始条件确定出来的解,称为其特解.
选项:
A: 正确
B: 错误
答案: 【 错误】
3、判断题:
微分方程的通解就是微分方程的所有解.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、判断题:
微分方程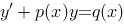 的通解为
的通解为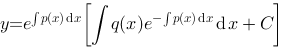 .
.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、判断题:
微分方程初值问题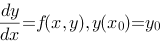 的解对应经过点
的解对应经过点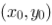 的一条积分曲线.
的一条积分曲线.
选项:
A: 正确
B: 错误
答案: 【 正确】
2、判断题:
所有微分方程的过一定点的积分曲线都是唯一的.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、单选题:
下列微分方程是伯努利方程的是( ).
选项:
A: 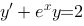
B: 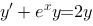
C: 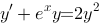
D: 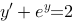
答案: 【 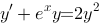 】
】
2、判断题:
方程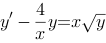 不是伯努利方程.
不是伯努利方程.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、判断题:
如果 是特征方程
是特征方程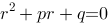 的二重根,则二阶常系数非齐次线性微分方程
的二重根,则二阶常系数非齐次线性微分方程 的特解形式为
的特解形式为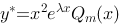 ,其中
,其中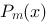 和
和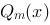 均为实系数
均为实系数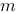 次多项式.
次多项式.
选项:
A: 正确
B: 错误
答案: 【 正确】
2、判断题:
微分方程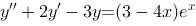 的一个特解具有形式
的一个特解具有形式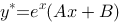 .
.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、单选题:
在空间直角坐标系中,点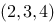 关于
关于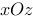 平面的对称点的坐标为( ).
平面的对称点的坐标为( ).
选项:
A: 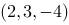
B: 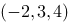
C: 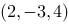
D: 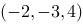
答案: 【 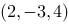 】
】
2、单选题:
点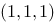 关于z轴的对称点的坐标为( ).
关于z轴的对称点的坐标为( ).
选项:
A: 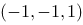
B: 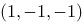
C: 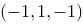
D: 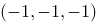
答案: 【 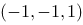 】
】
3、判断题:
在空间直角坐标系中,点与有序三元数组之间存在一一对应的关系.
选项:
A: 正确
B: 错误
答案: 【 正确】
1、判断题:
函数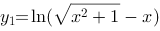 与
与 在
在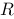 上线性无关.
上线性无关.
选项:
A: 正确
B: 错误
答案: 【 错误】
2、判断题:
定义在区间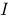 上的
上的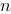 个函数
个函数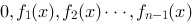 在区间
在区间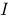 上一定线性相关.
上一定线性相关.
选项:
A: 正确
B: 错误
答案: 【 正确】
1、单选题:
微分方程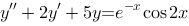 的一个特解具有形式( ).
的一个特解具有形式( ).
选项:
A: 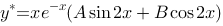
B: 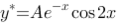
C: 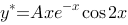
D: 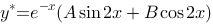
答案: 【 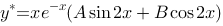 】
】
2、判断题:
对于二阶常系数非齐次线性微分方程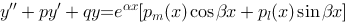 ,
,
若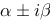 是特征方程
是特征方程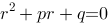 的根,则原方程的特解形式为
的根,则原方程的特解形式为
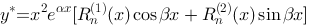 ,其中
,其中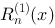 和
和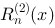 均为次数不超过
均为次数不超过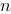 的多
的多
项式,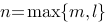 .
.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、单选题:
在空间直角坐标系中,点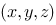 到
到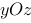 面的距离为( ).
面的距离为( ).
选项:
A: 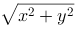
B: 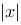
C: 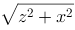
D: 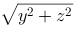
答案: 【 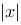 】
】
2、单选题:
在空间直角坐标系中,点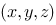 到
到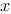 轴的距离为( ).
轴的距离为( ).
选项:
A: 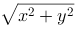
B: 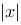
C: 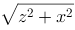
D: 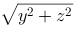
答案: 【 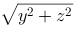 】
】
3、判断题:
在空间直角坐标系中,已知点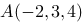 ,设点
,设点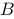 为点
为点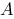 关于原点的对称点,则
关于原点的对称点,则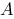 、
、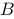
两点之间的距离为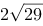 .
.
选项:
A: 正确
B: 错误
答案: 【 正确】
1、判断题:
设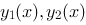 是非齐次线性方程
是非齐次线性方程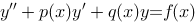 的两个解,则
的两个解,则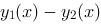 是齐次线性方程
是齐次线性方程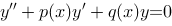 的解.
的解.
选项:
A: 正确
B: 错误
答案: 【 正确】
2、判断题:
方程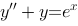 的通解为
的通解为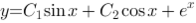 .
.
选项:
A: 正确
B: 错误
答案: 【 错误】
1、单选题:
对于无阻尼强迫振动微分方程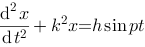 ,若
,若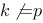 ,则其通解具有形式( ).
,则其通解具有形式( ).
选项:
A: 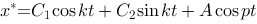
B: 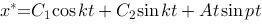
C: 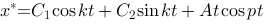
D: 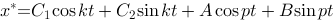
答案: 【 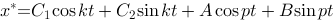 】
】
1、判断题:
向量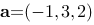 的模为
的模为 .
.
选项:
A: 正确
B: 错误
答案: 【 错误】
2、判断题:
在三维向量空间中,向径与空间中的点一一对应.
选项:
A: 正确
B: 错误
答案: 【 正确】
3、判断题:
如果向量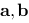 的大小相等,则称向量
的大小相等,则称向量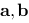 相等,并记作
相等,并记作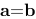 .
.
选项:
A: 正确
B: 错误
答案: 【 错误】
4、判断题:
如果两个非零向量平行,则这两个向量的方向要么相同,要么相反.
选项:
A: 正确
B: 错误
答案: 【 正确】
5、判断题:
在空间直角坐标系中,如果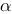 、
、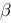 和
和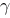 分别是某个非零向量关于
分别是某个非零向量关于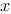 轴、
轴、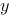

备案号:冀ICP备20010840号 2020-2099辉辉网络科技 All Rights Reserved